La Théorie du Dédoublement de l’Espace et du Temps
POURQUOI UN DÉDOUBLEMENT ?
Caractérisé par un mouvement, une curieuse vitesse et une équation universelle, le dédoublement de l’espace et du temps explique à la fois l’infiniment petit de nos particules, l’infiniment grand de l’univers… et nous, perdus sur une terre immense, planète d’un tout petit système solaire dont les dimensions nous semblent infinies.
Il nous suffit d’admettre qu’il puisse exister des temps imperceptibles, coincés entre deux temps perceptibles.
Le temps entre une question (un obstacle quelconque) et sa réponse (franchissement de l’obstacle) définit un temps d’adaptation pour une particule, qui utilise ce temps dans son espace défini et limité par son horizon. Une accélération de l’écoulement du temps dans un horizon imperceptible, dédoublé du premier horizon, permet à une particule, dédoublée de la particule initiale, évoluant de la même façon, d’obtenir la réponse avant la particule initiale.
L’accélération du temps peut être telle que la particule initiale « n’a pas le temps » d’utiliser un « instant » de son temps pendant que la particule dédoublée « a tout le temps » d’obtenir la réponse à sa question « dans ce même instant ». Cela nécessite la possibilité d’accélérer le temps tout en dédoublant la particule initiale dans des temps imperceptibles que j’ai appelés « ouvertures temporelles ».
Or le temps est observable et mesurable par le mouvement d’un espace par rapport à un autre. Il est de ce fait continu. Différencier le temps dans des « ouvertures temporelles » revient à différencier l’observation d’un mouvement, donc la perception de l’observateur lui-même, qui est à la fois horizon de particules et particule dans son horizon.
Le dédoublement implique un observateur dédoublé, évoluant dans les ouvertures temporelles de l’observateur initial. Du fait d’une différence de perception, l’observateur dédoublé évolue rapidement dans un temps accéléré qu’il considère comme normal.
Il ignore alors l’observateur initial puisqu’il ignore son temps d’évolution qui lui semble figé.
Il peut se considérer comme un observateur initial qui a son tour se dédouble. Un 3ème observateur répond donc aux questions du 2ème en se posant lui aussi d’autres questions.
Par des échanges d’information dans des « ouvertures temporelles » imperceptibles, le 1er observateur peut obtenir des réponses à des questions qu’il n’a pas eu le temps de se poser. Cela lui permet de connaître les réponses du 3ème avant le 2ème qu’il peut donc guider en lui suggérant de nouvelles questions qui modifient sa mémoire instantanément.
Autrement dit, le 2ème observateur évolue dans son présent. Il répond aux questions du 1er qui lui semble provenir du passé. Il se pose des questions auxquelles le 3ème répond à son tour. Ces réponses semblent être dans son futur. Par les échanges d’information instantanés dans les ouvertures temporelles, il est donc, en même temps, observateur dans trois temps différents : passé, présent, futur.
La théorie du dédoublement donne une équation qui permet d’exprimer de façon rigoureuse le changement de perception entre deux observateurs dédoublés dans deux temps différents.
Cette équation est la base fondamentale de la théorie du dédoublement. Par un changement d’échelle d’espace et de temps, elle réunit l’infiniment grand d’un observateur initial et l’infiniment petit de l’observateur dédoublé.
LE MOUVEMENT DE DÉDOUBLEMENT
Tout part d’un cercle Ω qui tourne sur lui-même. Son rayon tourne avec une vitesse de rotation constante φ :
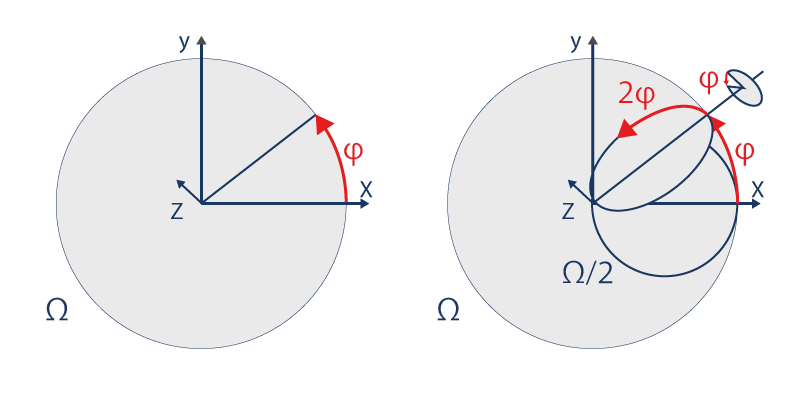
Or ce rayon est le diamètre d’un cercle Ω/2 deux fois plus petit qui tourne sur lui-même deux fois plus vite, tout en tournant dans l’espace, autour de son diamètre avec la même vitesse φ. Ce cercle Ω est comme un manège. En y prenant place, le cercle Ω/2 suit le mouvement, mais en tournant sur lui-même, tout en faisant la pirouette.
Ce mouvement fondamental se poursuit avec le cercle Ω/4 = 2α deux fois plus petit que le cercle Ω/2, lui-même deux fois plus petit que le cercle Ω…
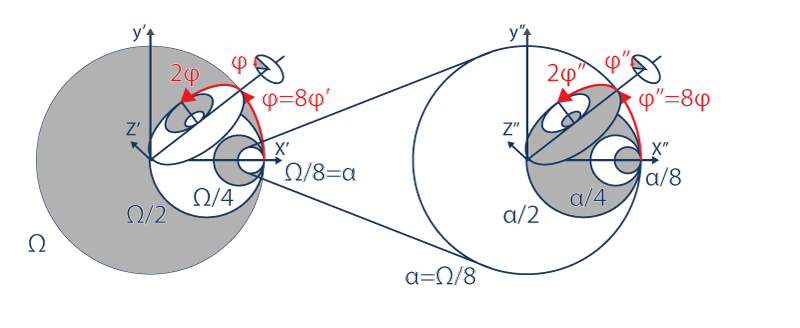
Et ainsi de suite dans l’infiniment petit :
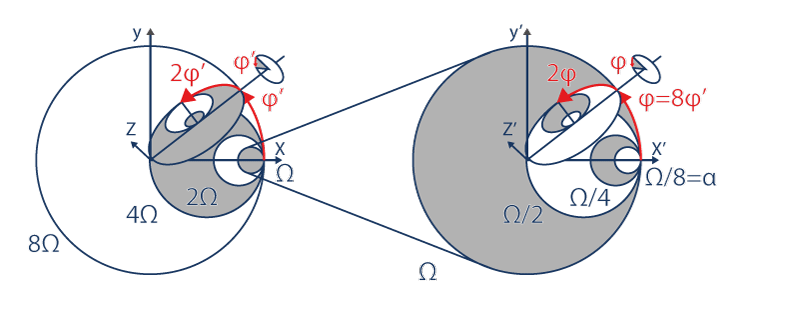
Comme dans l’infiniment grand :
Une visualisation du mouvement par ordinateur nous montre les trajets des particules sur les différents cercles emboîtés dans le même mouvement :
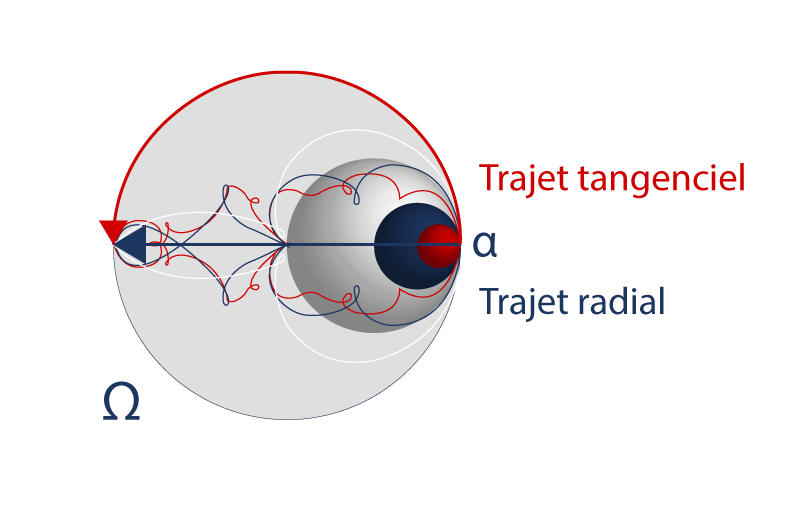
Mis à part le trajet tangentiel qui fait le tour, tous les autres trajets passent par le centre. D’où la logique des appellations : trajet radial et trajet tangentiel.
L’équation du mouvement est :
X = cos²φ(cosφ – sin²φ) Y = cos²φsinφ(1 + cosφ) Z = – cosφsin²φ
Certes, les courbes radiales sont un peu compliquées, mais en réalité, seuls sont importants le début et la fin du dédoublement de la particule α dans son horizon Ω. On peut donc représenter d’une façon très schématique ce mouvement de dédoublement sur l’axe de l’horizon Ω :
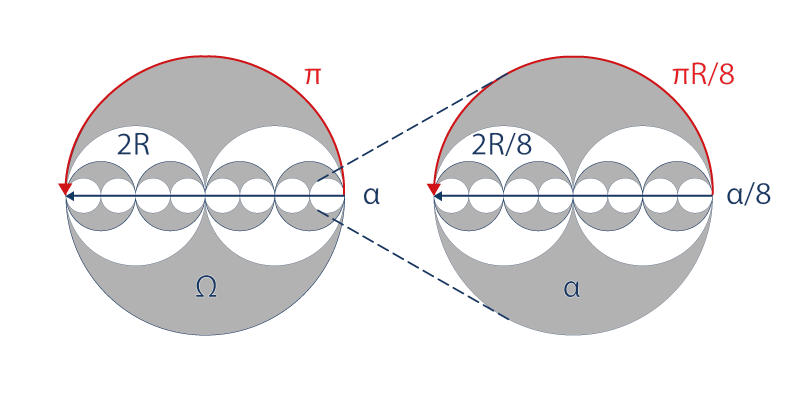
On pourra dire que ce mouvement de dédoublement est universel dans l’infiniment petit comme dans l’infiniment grand si la particule α est l’horizon de sa particule α/8 et si son horizon Ω est la particule de son propre horizon 8Ω.
Cette loi du dédoublement pourrait donc être appelée « La loi de l’alpha et de l’oméga », une loi qui dirige les étoiles, les planètes, l’étonnant Big-bang – aussi mal compris que l’inflation initiale – l’accélération apparente actuelle de l’expansion de l’univers… et sa contraction prochaine !
Une loi qui, de toute évidence, nécessite une intelligence suprême, capable de la mettre en application et qui serait à la fois l’alpha et l’oméga, le commencement et la fin !
Dans l’infiniment petit, l’énergie n’arrive pas de façon continue.
Elle est distribuée de façon discontinue par des « quanta » d’énergie : chaque « quantum » étant séparé du suivant par un temps imperceptible, quasi nul, mais où les particules disposent cependant d’une énergie infinie. C’est le fameux « Principe d’Heisenberg » : pour simplifier, disons que, pour une particule, l’énergie disponible, multipliée par le temps perceptible mais quasi nul de cette disponibilité est supérieure ou égale à la constante de Planck. Il en résulte que, si ce temps semble nul pour un observateur, cette énergie lui paraît infinie. En réalité, le temps nul n’existe pas…
Cette succession de quanta d’énergie donne l’impression d’une continuité pour les observateurs que nous sommes. Il n’en est rien ! D’où l’appellation de mécanique « quantique » pour l’infiniment petit des particules.
Le dédoublement se justifie facilement par l’idée suivante : une particule se dédouble pour s’introduire à l’intérieur d’un univers et y acquérir de nouvelles connaissances, tout en le contournant, gardant ainsi intacte sa mémoire. Mais cela ne s’arrête pas là ! Nous avons vu que la particule dédoublée en fait autant avec un univers deux fois plus petit et ainsi de suite…
C’est ainsi qu’un trajet tangentiel est aussi un trajet radial qui passe par le centre d’un univers deux fois plus grand. De même, un trajet radial est un trajet tangentiel d’un univers deux fois plus petit.
On peut toujours dire que, dédoublée d’une particule tangentielle, une « particule radiale », est une « particule tangentielle » qui se dédouble pour explorer sans danger un univers deux fois plus petit.
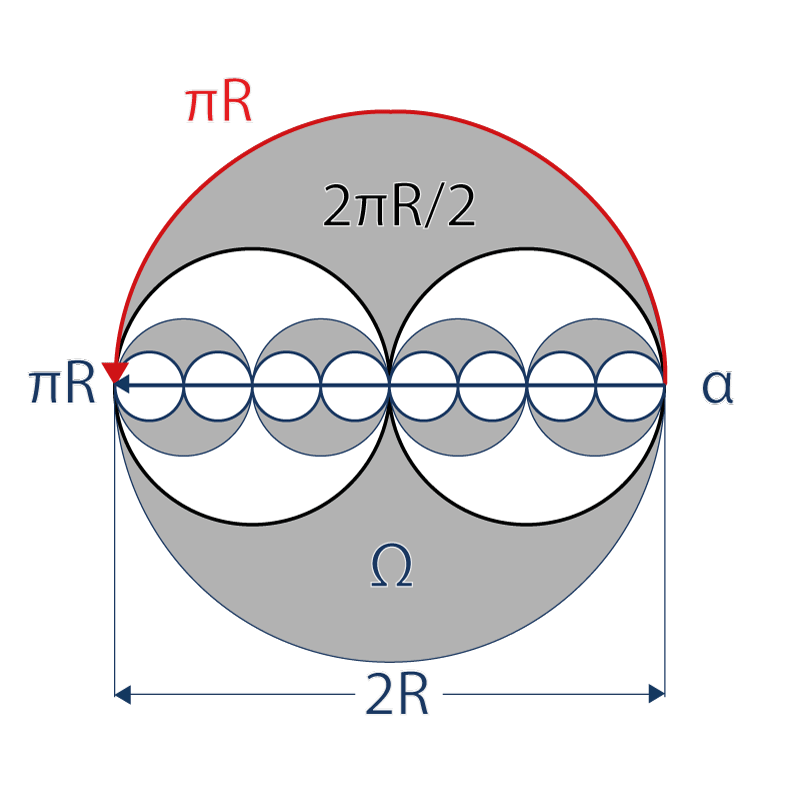
Cependant, il sera intéressant de savoir pourquoi, quand et comment ce dédoublement est limité dans le temps et dans l’espace.
Dans l’horizon initial, nous avons vu que le trajet radial d’un trajet tangentiel est donc toujours égal à πR, si 2R est le diamètre du trajet tangentiel initial et π = 3,14… Dit irrationnel, ce nombre sans fin existe dans un point, petit rien du tout circulaire de rayon quasi nul. Il existe aussi avec une droite qui est un cercle de rayon infiniment grand ou encore un horizon tangentiel lointain.
On peut dire plus simplement qu’un trajet radial est le diamètre d’un horizon. Il est constitué d’une succession de n petits cercles de rien du tout. Le diamètre de Ω est égal à 2R pour un observateur externe qui considère ce cercle comme l’horizon d’une petite particule ; il doit être égal à πR pour un observateur interne qui considère ce même cercle comme l’horizon lointain de son univers immense.
En effet, à travers un horizon Ω, un trajet radial est constitué schématiquement d’une succession de n petits cercles α (trajets radiaux), de rayon R/n, où n est un nombre entier. Quel que soit n, il est égal à nπR/n = πR :
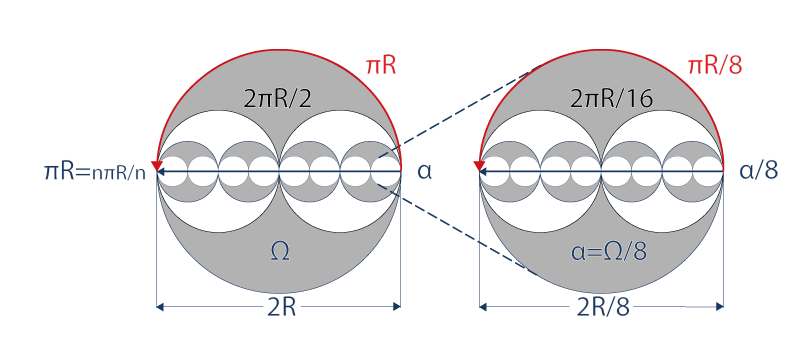
ÉQUATION DU DÉDOUBLEMENT
Accélérer le mouvement de dédoublement et dilater un espace pour le rendre imperceptible dans l’espace initial n’est intéressant que si l’observateur de l’espace initial se dédouble également dans l’espace imperceptible. Ainsi, tout en restant l’observateur de l’espace initial, son « double » peut observer l’espace dédoublé dans un temps qui n’a pas le temps d’exister dans l’espace initial.
Il est donc indispensable de connaître la relation qui permet de changer d’observation entre deux espaces dédoublés, évoluant dans deux temps différents mais dans le même plan d’observation.
La théorie du dédoublement repose sur une équation universelle permettant de passer de l’observateur interne (qui parcourt un trajet radial égal à πR dans un espace dilaté et accéléré) à l’observateur externe (pour qui ce même trajet radial est le diamètre de ce même espace : un diamètre égal à 2R) :
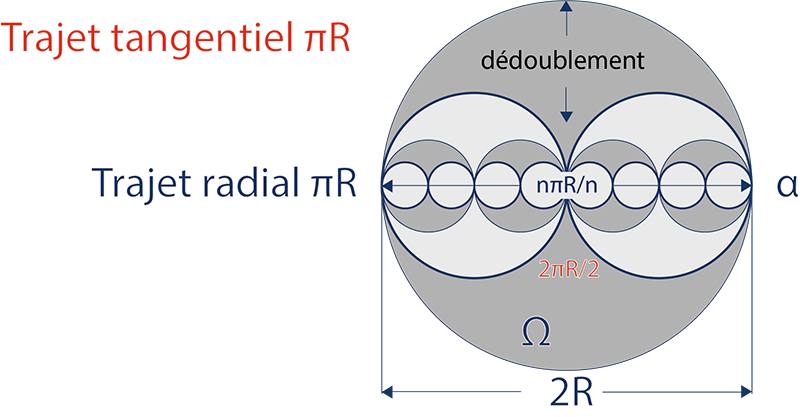
L’observateur interne ignore le diamètre 2R de son horizon dilaté Ω’ qui est devenu égal à l’horizon initial Ω dans le plan initial, mais dans un temps imperceptible de l’observateur initial.
Pour l’observateur interne, ce diamètre D est le trajet radial πR d’une particule qui tourne sur elle-même :
D = πR.
Correspondant à ce diamètre D, l’horizon apparent lui apparait donc comme étant la demie circonférence, qui comme toute demie circonférence est égale à ½ πD.
Donc pour cet observateur interne, on a la relation :
½ πD = ½ π(πR) = π²R/2.
Cependant, la rotation π perçue par l’observateur interne correspond, pour l’observateur externe, au diamètre apparent 2R de l’horizon Ω.
Ainsi (π²)⁻ pour l’observateur interne, noté (-),
Devient (4R²)⁺ pour l’observateur externe, noté (+).
Or le rayon R, perçu par l’observateur externe est, pour l’observateur interne, égal au trajet radial π/8 du fait de la dilatation de la particule qui devient 8 fois plus grosse lors d’une 9ème rotation π/8.
Ainsi (R/2)⁺ pour l’observateur externe (+),
Devient (π/16)⁻ pour l’observateur interne (-).
Donc : [(π²)(R/2)]⁺ devient [(4R²)( π/16)]⁻ = (πR²/4)⁻.
Or l’observateur externe (+) perçoit la ½ circonférence πR, on en déduit que (πR²/4)⁻ de l’observateur interne (-) est égal à (πR)⁺ de l’observateur externe (+).
D’où l’équation fondamentale du changement de perception du temps et de l’espace entre l’observateur interne (-) et l’observateur externe (+) :
(πR²)⁻ = (4πR)⁺
En considérant la variable R et en dérivant le premier membre de l’équation πR², on n’obtient que la moitié du second membre :
(4πR)/2.
Où est donc passé l’autre moitié ? Il ne faut pas oublier que le mouvement de rotation s’accélère, π devenant 2π dans un temps imperceptible et dans un espace 2 fois plus grand où le résultat devient juste et observable dans le temps de l’observateur.
Le langage mathématique permet de le dire d’une autre façon :
En considérant la variable R et en dérivant le premier membre de l’équation πR², on obtient la moitié du second membre 2πR. Inversement, en intégrant 2πR, on retrouve πR². Mais ce rayon R est une constante ! Or la dérivation d’une constante donne zéro et l’intégration de zéro – opération apparemment inverse – n’existe pas… sauf si zéro n’existe pas !
Dans ce dédoublement du temps, l’intégration concerne toujours un nombre infiniment petit. Il faudrait donc que la dérivation d’une constante donne une autre constante infiniment petite et imperceptible dans notre temps, ce qui n’est évidemment pas admis en mathématique actuellement où zéro reste un zéro absolu. Mais il n’en reste pas moins que dans l’univers, du fait du dédoublement du temps, le zéro absolu ne peut exister, sinon l’observation n’est plus possible et, de ce fait, l’observateur devient totalement inutile.
Tous les mathématiciens de l’antiquité savaient que le zéro n’existait pas. Ne serait-ce pas la conséquence de la connaissance du mouvement de dédoublement ?
LA VITESSE DE LA LUMIÈRE
Par une vérification du mouvement de dédoublement dans notre système solaire et une justification rigoureuse des mouvements planétaires, conforme au mouvement fondamental de dédoublement défini dans la théorie, la vitesse de la lumière a pu être justifiée et surtout calculée pour la 1ère fois(publications 1998).
C₀ = trajet radial / trajet tangentiel = 2(108πDs)10⁴ / 1 an = 299 792 km/s
Avec le diamètre du Soleil : Ds = 1 394 180 km.
La vitesse de la lumière est la constante universelle du mouvement de dédoublement. De ce fait, le diamètre apparent de notre Soleil doit absolument correspondre à cette valeur pour les observateurs que nous sommes dans notre système solaire : c’est le cas à l’heure actuelle. Comme nous le verrons, une modification de ce diamètre entraîne obligatoirement une modification du trajet radial de la Terre (distance aphélie-périhélie) sans modifier le trajet tangentiel (1/2 année) qui nous donne la mesure de notre temps. Cette modification peut avoir des conséquences chaotiques pour la Terre et dans tout le système solaire.
On comprend enfin l’importance fondamentale de cette théorie du dédoublement du temps qui met le diamètre de notre Soleil au premier rang de notre observation terrestre.
Il en est de même des vitesses supraluminiques, nécessaires au dédoublement du temps. En effet, le mouvement de dédoublement les impose, et permet leur calcul (publiées en 1998) : C₂ = 7C₁ = (7³/12)10⁵C₀, où C₀ est la vitesse de la lumière.
Ce rapport des vitesses limite l’espace et le temps du dédoublement. Á la fin du cycle apparaît une 3ème vitesse supraluminique C₃ = 7C₂ qui ouvre notre monde sur l’imperceptible. Nous verrons que cette limite impose un nombre fini de 2èmes observateurs dédoublés du 1er. Elle impose aussi un seul dédoublement du 2ème qui aura donc un seul double pour répondre à ses questions.
En établissant l’équation de la vitesse de la lumière, il m’a été possible d’expliquer de façon rigoureuse le curieux postulat introduit par Einstein affirmant sans justification logique que la vitesse de la lumière était indépendante de la vitesse de la source et de la vitesse de l’observateur. En effet, C₀ est la vitesse de perception du temps présent dans un horizon d’observation où tous les différents observateurs de ce même horizon doivent percevoir toutes les informations en même temps pour faire partie de la même réalité présente. Ce synchronisme d’observation est indispensable pour qu’il puisse exister un présent commun aux différents observateurs évoluant dans le même horizon et le même temps.
Les postulats disparaissent
Pour accélérer le temps, il faut obligatoirement utiliser des vitesses plus grandes que C₀. Dites super-lumineuses, ces vitesses donnent à d’autres observateurs dédoublés la possibilité de percevoir la réalité plus rapidement. Depuis quelques années, des scientifiques (A. Aspect 1982, N. Gisin 1998, A. Suarez 2002) ont observé ces vitesses sans pouvoir justifier leur existence. Cette justification semblait impossible car, d’après l’équation d’Einstein (E=mC²), une particule devait avoir une masse nulle pour atteindre la vitesse de la lumière. Comme une information est une énergie E, elle possède donc une masse m = E/ C² qui, du fait de cette équation, ne peut aller plus vite que la lumière.
On peut expliquer cela autrement avec la théorie du dédoublement :
- Une masse nulle dans un horizon, passe dans un horizon imperceptible avec une vitesse superluminique dans un temps imperceptible défini par le mouvement de dédoublement (que j’ai appelé « ouverture temporelle ») où elle possède une masse.
- Une information qui dépasse la vitesse de la lumière change de temps. C’est une loi mise en évidence par Langevin en 1923 (principe des jumeaux de Langevin) et vérifiée expérimentalement en 1972 par Kneferle et Keating.
- Un changement d’échelle montre qu’un potentiel à l’extérieur d’un horizon exprimé en 1/L (où L est une mesure d’espace), devient une force en 1/L² pour les particules de cet horizon.
- Une onde infiniment grande dans un horizon devient une onde infiniment courte dans un autre où le temps est accéléré et où l’observateur n’a plus la même perception du temps. On a pu montrer qu’au zéro absolu (-273°K), un atome perdait son côté corpusculaire. Ne restait que l’information ondulatoire. C’était prévu mais non vérifié par Einstein, Podolsky, Rosen.
Les trois énergies de dédoublement. Toutes ces propriétés permettent de faire évoluer dans le même univers des réalités (passé, présent, futur) qui ne se perçoivent pas et qui sont dépendantes de trois vitesses et de trois énergies de dédoublement dont la théorie du dédoublement donne les rapports : 0,1%, 33,3% et 66,6% de l’énergie initiale.
En 1998, Saul Perlmutter et Brian Schmidt ont montré, chacun de leur côté, par l’observation d’une supernova, qu’il existait une énergie de répulsion inconnue correspondant à 66,7% de l’énergie de l’univers : en 2012, ils ont reçu le prix Nobel. Cette observation est venue confirmer le théorème des trois énergies de la théorie du dédoublement. En son temps, Albert Einstein a essayé d’introduire une constante cosmologique de 67%. N’ayant pu la démontrer, il a déclaré, deux ans avant sa mort, que cette constante était « la plus grande erreur de sa vie », alors qu’en fait, elle provenait d’une intuition géniale. En plus de l’observation de ces deux prix Nobel, la théorie du dédoublement lui donne raison.
C’est en accélérant le mouvement de doublement dans un plan qui se dilate que l’on peut changer de temps dans un espace à trois dimensions observables.
