The doubling Theory

Everything starts from a circle Ω, which turns on itself. His radius turns with a constant rotation speed φ:

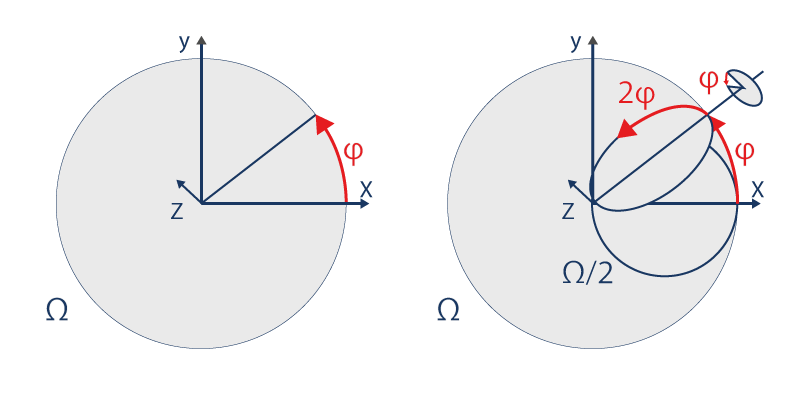
However, this radius is the diameter of a circle Ω/2 two times smaller, which turns on itself two times faster, while turning in space, around his diameter with the same speed φ. This circle Ω is like a carousel. By taking its place in it, the circle Ω/2 follows the movement, while turning on itself and spinning like a top.
This fundamental movement goes on with the circle Ω/4 = 2α two times smaller than the circle Ω/2, two times smaller itself than the circle Ω…

It goes on and on in the infinitely small:

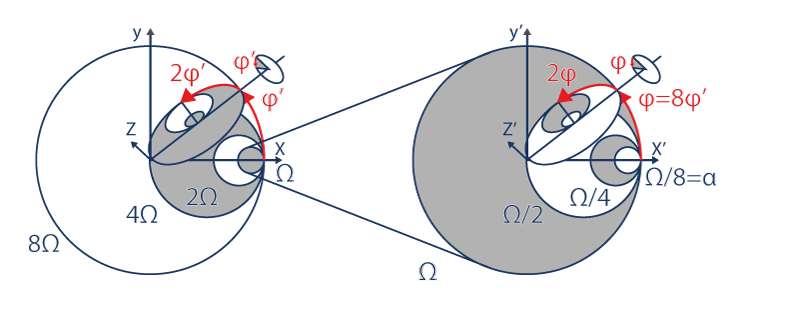
As in the infinitely large:

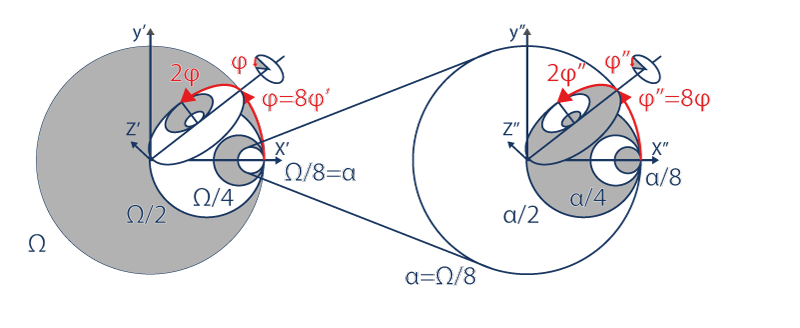
The visualization of the movement with a computer shows us the particle’s paths on the different circles nested in the same movement:

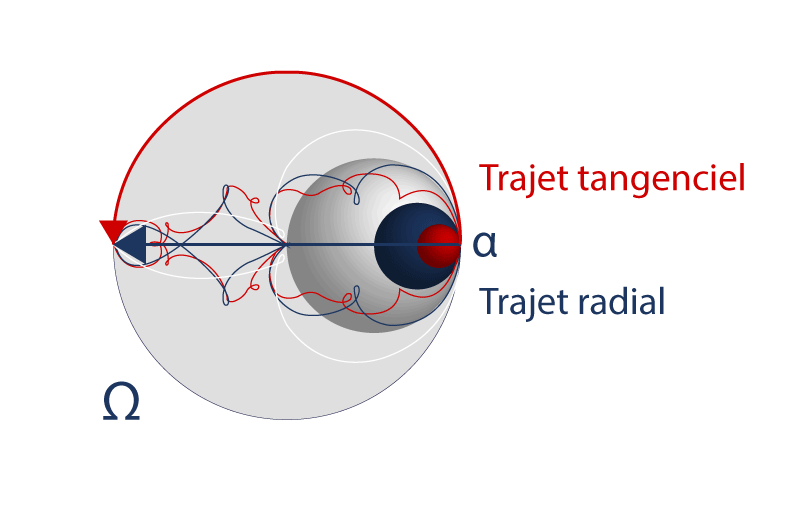
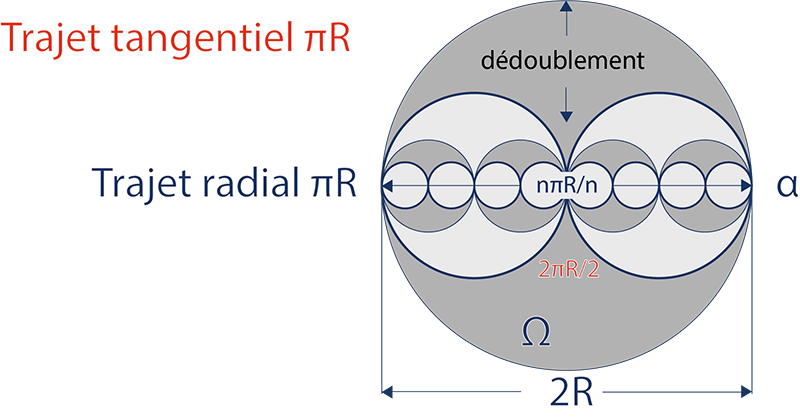
Aside from the tangential path which goes around, all the other paths go through the center point. Hence the logical names: “radial” and “tangential” paths.
The movement equation is:

X = cos²φ(cosφ – sin²φ)   Y = cos²φsinφ(1 + cosφ)   Z = – cosφsin²φ

The radial curves are definitely complicated, but actually, only the beginning and the end of the doubling of the particle α in its horizon matter. We can represent in a very schematic way this Doubling movement on the axis of the horizon Ω:

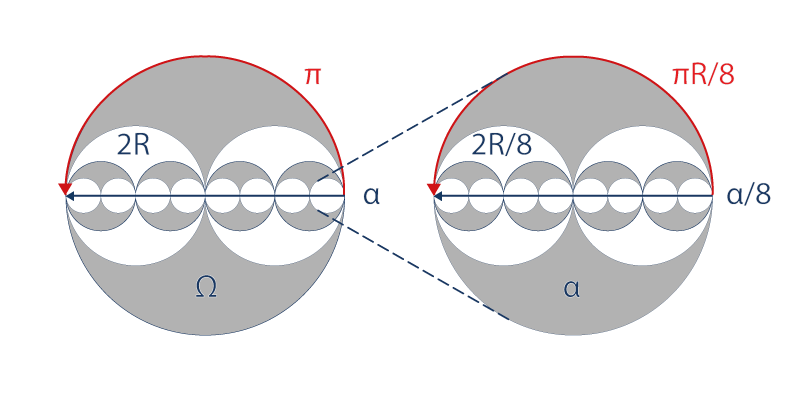
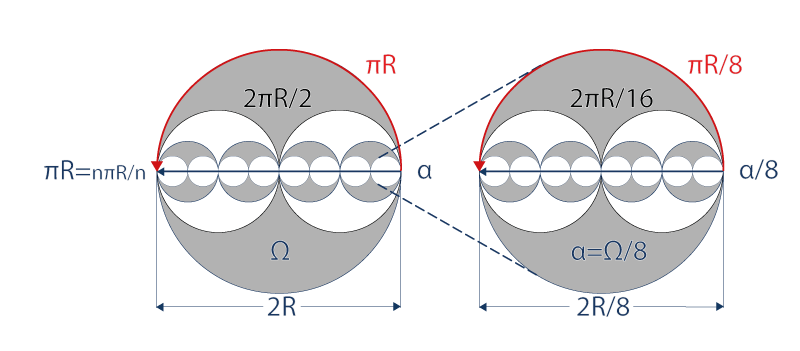
One may say that this Doubling movement is universal in the infinitely small as in the infinitely large if the particle α is the horizon of its particle α/8 and if its horizon Ω is the particle of its own horizon 8Ω.

This Doubling law could also be called « The law of the alpha and the omega », a law that governs the stars, the planets, the stunning Big-bang – as misunderstood as the general inflation–  the current apparent acceleration of the Universe expansion… and its upcoming contraction!
A law which clearly needs a supreme intelligence, an intelligence which is able to put this law into effect and which would be both the alpha and the omega, and both the beginning and the end!
In the infinitely small, the energy isn’t continuous. She’s distributed in a discontinued way by “quanta” of energy: each “quantum” being separated from the next one by an imperceptible time, a practically null time, but where the particles have an infinite energy. This is the famous “Heisenberg’s Principle”. In order to simplify, let’s just say that: for a particle, the energy available multiplied by the practically null perceptible time of this availability, is superior or equal to the constant of Planck. As a result, if this time seems to be null for an observer, this energy appears to him to be infinite. Actually, the null time doesn’t exist… This succession of quanta of energy gives the impression of a continuity for the observers that we are. It’s nothing like that! That is why we call the mechanics “quantum” for the infinitely small of the particles.
Doubling justifies itself easily by the following idea: a particle doubles itself to get into a universe to improve its knowledge, while skirting it in order to keep its memory intact. But it isn’t just that! We saw that the doubled particle does the same thing with a universe two times smaller and on and on…

It is in this way that a tangential path is also a radial path leading to the center point of a universe two times bigger. As well as the radial path which is a tangential path of a universe two times smaller.

We can always say that: doubled from a tangential particle, a “radial particle”, is a “tangential particle” which doubles itself to explore without any danger a universe two times smaller.
However, it would be interesting to know why, when and how this Doubling is limited in time and space.
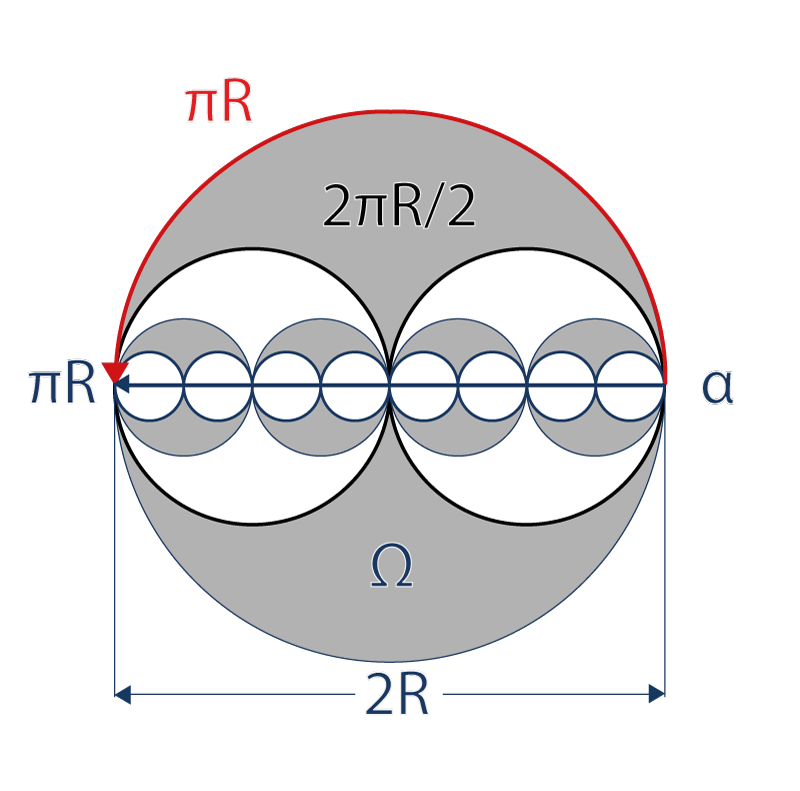
In the initial horizon, we saw that the radial path of a tangential path always equals to πR, if 2R is the diameter of the initial tangential path and π = 3,14…  Considered as irrational, this no end number exists in a point of a diameter practically null. It also exists with a straight line that is a circle with an infinitely large radius or a distant tangential horizon.
More simply, we can say that a radial path is the diameter of a horizon. He’s composed of a succession of n tiny circles. The diameter of Ω equals to 2R for an external observer who considers this circle as the horizon of a small particle; it must equals to πR for an internal observer who considers this same circle as the distant horizon of its huge universe.

In fact, through a horizon Ω, a radial path is schematically constituted of a succession of n tiny circles α (radial paths), with a radius R/n, where n is a whole number. Whatever n is, it equals to nπR/n = πR: 

Accelerating the Doubling movement and dilating a space in order to make him imperceptible in the initial space is interesting only if the observer of the initial space also doubles himself in the imperceptible space. Then, while staying the observer of the initial space, his “double” can observe the doubled space in a time that “hasn’t the time” to exist in the initial space. It is therefore essential to know the relation which allows to change the observation between two doubled spaces, evolving in two different timescales but in the same observation plan.

The Doubling theory is based on a universal equation allowing the change from the internal observer (traveling through a radial path equaling to πR in a dilated and accelerated space) to the external observer (for whom this same radial path is the diameter of this same space: a diameter equaling to 2R):

The internal observer ignores the diameter 2R of its dilated horizon Ω’ who became equal to the initial horizon Ω in the initial plan, but in an imperceptible time of the initial observer.

For the internal observer, this diameter D is the radial path πR of a particle who turns on itself:

D = πR.

Corresponding to this diameter D, the apparent horizon appears to him as the half circumference which, as any other half circumstance equals to ½ πD.

So for this internal observer, we have the relation:

½πD = ½ π(πR) = π²R/2.

However, the rotation π viewed by the internal observer corresponds, for the external observer, to the apparent diameter 2R of the horizon Ω.

Then (π²)⁻ for the internal observer (-),

Becomes (4R²)⁺ for the external observer (+).

But the radius R, seen by the external observer, equals to the radial path π/8 because of the dilatation of the particle which becomes 8 times bigger during a 9th rotation π/8.

Then (R/2)⁺ for the external observer (+),

Becomes (π/16)⁻ for the internal observer (-).

So: [(π²)(R/2)]⁺ becomes [(4R²)( π/16)]⁻ = (πR²/4)⁻.

However the external observer (+) perceives the ½ circumference πR, we can deduce that (πR²/4)⁻ from the internal observer (-) equals to (πR)⁺ from the external observer (+).

Hence the fundamental equation of the change of perception of the time and of the space between the internal observer (-) and the external observer (+):

(πR²)⁻ = (4πR)⁺

By considering the variable R and by deriving the first member of the equation πR², we only get the half of the second member: (4πR)/2.

Where did the other half go? We mustn’t forget that the rotation movement accelerates, π becoming 2π in an imperceptible time and in a space two times bigger where the result becomes right and observable in the time of the observer.

The mathematical language allows another way of saying it:

By considering the variable R and by deriving the first member of the equation πR² we get the half of the second member 2πR. Inversely, by integrating 2πR, we find again πR². But this radius R is a constant! And the derivation of a constant gives zero and the integration of zero – apparently opposite operation – doesn’t exist… except if zero doesn’t exist!

In this doubling of time, the integration always concerns an infinitely small number. The derivation of a constant should give another infinitely small constant as well as imperceptible in our time. That is obviously still not admitted in mathematics where zero stays an absolute zero. But what remains clear in the universe, because of the doubling of time, is that the absolute zero can’t exist, otherwise the observation would be no more possible, and from this fact, the observer would become useless.

All the mathematicians during Antiquity knew that zero didn’t exist. Wouldn’t it be the consequence of the knowledge of the Doubling movement?

By a verification of the Doubling movement in our solar system and a rigorous justification of the planetary movements, by a compliance with the fundamental Doubling movement defined in the theory, the speed of Light has been justified and above all calculated for the first time (1998 publications).

C₀ = trajet radial / trajet tangentiel = 2(108πDs)10⁴ / 1 an = 299 792 km/s

With the sun diameter: Ds = 1 394 180 km.

The speed of light is the universal constant of the Doubling movement. Hence, the apparent diameter of the Sun must absolutely match this value for the observers that we are in our solar system: as is currently the case. As we shall see, a modification of this diameter will naturally entail a modification of the radial path of the Earth (the distance aphelion-perihelion) without altering the tangential path (1/2 year) which gives us the measurement of our time. This modification can lead to chaotic consequences for the Earth and the entire solar system.

We finally understand the fundamental importance of this Time Doubling theory which puts the sun diameter at the first rank of the Earth observation.  

Superluminal speeds, are necessary to the Doubling of Time. They are imposed by the Doubling movement, which allow their calculation (published in 1998):  

C₂ = 7C₁= (7³/12)10⁵C₀, where C₀ is the speed of Light.

This speed relation limits the time and the space of the Doubling

At the end of the cycle appears a 3rd superluminal speed C₃ = 7C₂ which opens our world on the “imperceptible”. We’ll see that this limit imposes a finite number of second observers doubled from the first one. She also imposes only one doubling of the second observer who will only have one double to answer his questions.
By establishing the equation of the speed of Light, I have been able to explain rigorously the curious postulate introduced by Einstein who affirmed without any logical explanation that the speed of Light was independent from the source’s speed and from the observer’s speed.

C₀ is the speed of perception of the time existing in a horizon of observation where all the different observers of this same horizon must perceive all the information at the same time to be a part of the same present reality. This synchronism of observation is indispensable so that he can exist in a present common to the different observers existing in the same horizon and the same time.

The postulates disappear

To accelerate the time, speeds faster than C₀ must be used. Called superluminal ones, thoses speeds give other doubled observers the possibiliy to perceive the reality faster. Since a few years, Scientifics (A. Aspect 1982, N. Gisin 1998, A. Suarez 2002) observed those speeds without being able to justify their existence. This justification seemed impossible because, according to Einstein’s equation (E=mC²), a particle should have a null mass to reach the speed of Light. As an information is an energy E, she therefore owns a mass m = E/ C² which, because of this equation, cannot go faster than the speed of Light.

We can explain this on another way with the Doubling theory:

• A null mass in a horizon, runs in an imperceptible horizon with a superluminal speed in an imperceptible time defined by the Doubling movement (that I called « time openings ») where she owns a mass.
• An information, that is faster than the Speed of Light, changes time. This law was demonstrated by Langevin in 1923 (the Langevin twins principle) and was experimentally verified in 1972 by Kneferle and Keating.
• A timescale change potential outside a horizon expressed in 1/L (where L is a measurement of space) becomes a force in 1/L² for that horizon’s particles.  
• An infinitely large wave in a horizon becomes an infinitely short wave in another horizon in which time is accelerated and in which the observer does not have the same perception of time anymore. We were able to show that at the absolute zero (-273°K), an atom would lose his corpuscular side. Only the wave information would stay. It was expected but not verified by Einstein, Podolsky, Rosen.

The three doubling energies

All the above properties make it possible for the realities (past, present and future) to coexist, although they do not perceive each other, and are dependent upon the three speeds and the three doubling energies.  The doubling theory gives their relationships:

0,1%, 33,3% and 66,6% of the initial energy.

In 1998, Saul Perlmutter and Brian Schmidt, while observing a supernova, independently of each other, demonstrated the existence of an unknown repulsion energy, equaling to 66,7% of the energy of the universe: in 2012, they won a Nobel prize. This observation confirmed the doubling theory three-energy theorem. In his own epoch, Albert Einstein attempted to introduce the 67% cosmological constant. He was never able to prove it, and two years before he died, he declared that the constant was “the biggest mistake of his life”, whereas in fact, it was a brilliant stroke of intuition. The Doubling theory proves him right.

It is by accelerating the Doubling movement in a dilating plan that we can change the time in a three observable dimensions space.